Volviendo a los programas concurrentes, la elección o preferencia entre las alternativas de respuesta se calcula por la tasa relativa de respuesta y se representa por el cociente:
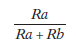
Donde Ra y Rb representan, respectivamente, la tasa de respuesta en la alternativa a y la tasa de respuesta en la alternativa b.
El procedimiento de los programas concurrentes presenta ventajas para medir la elección en el sentido de que se miden las preferencias de los sujetos por dos fuentes alternativas de reforzamiento pero para cuya consecución se requieren respuestas operantes semejantes (por ejemplo, presionar la palanca a ó presionar la palanca b).
Con anterioridad a los programas concurrentes, muchos investigadores utilizaron procedimientos que se podrían definir como de premios concurrentes, donde normalmente se daba a elegir a los sujetos entre dos actividades diferentes, como por ejemplo correr y beber, y se medía el tiempo que dichos sujetos experimentales empleaban en cada una de estas dos actividades conductuales. En base a los resultados que se obtenían, se inferían las preferencias relativas de los sujetos. Este procedimiento para medir la elección no es el más adecuado en muchas circunstancias pues la elección entre premios concurrentes presenta la dificultad de comparar entre sí dos actividades conductuales que implican respuestas consumatorias distintas. En los programas concurrentes, los sujetos ya no eligen directamente entre diferentes premios, sino que eligen entre distintas alternativas que requieren una respuesta operante idéntica pero que pueden llevar a premios diferentes. Este procedimiento, frente a la elección entre premios concurrentes, se puede denominar de elección entre respuestas instrumentales concurrentes, y específicamente es el utilizado en los programas concurrentes de reforzamiento.
La ley de igualación
La ley de igualación, formulada por Herrnstein al observar que los animales distribuían respuestas en función de la frecuencia de reforzamiento de cada alternativa, afirma que la tasa relativa de respuesta entre dos alternativas de respuestas concurrentes es igual a la tasa (frecuencia) relativa de reforzamiento asociada con cada una de dichas alternativas de respuesta, y quedó expresada matemáticamente por la Ecuación 5.1:
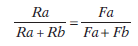
Donde Ra y Rb representan las tasas de respuesta en las alternativas a y b; y Fa y Fb representan la tasa (frecuencia) de reforzamiento asociada a las alternativas a y b respectivamente.
Los principales resultados encontrados por Herrnstein referidos a tres palomas (055, 231 y 641) relacionan la tasa relativa de respuesta en el eje de ordenadas con la tasa relativa de reforzamiento en el eje de abscisas (aquí referido a porcentaje de respuestas y reforzadores en la tecla A). La ley de igualación establece una equiparación entre la distribución de las tasas de respuesta en las alternativas a y b y la distribución de las tasas de reforzamiento en dichas alternativas de respuesta. En los casos extremos, y si el total de reforzadores se obtuviese en la alternativa a, también se darían el total de respuestas en dicha alternativa (sería el caso del vértice superior derecho). Si, por el contrario, el total de reforzadores se obtuviese en la alternativa b, sería en la alternativa b donde se darían todas las respuestas (vértice inferior izquierdo).
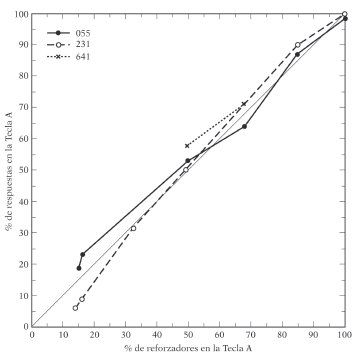
Si los reforzadores se distribuyesen al 50% entre las dos alternativas, la ley de igualación establece que las respuestas se distribuirían por igual entre las dos alternativas. Esta relación lineal entre la tasa relativa de respuesta y la tasa relativa de reforzamiento viene representada por la línea diagonal que divide el área de la figura en dos partes iguales.
Lo que Herrnstein encontró es que variando la frecuencia de reforzamiento asociada a las alternativas de respuesta por medio de la utilización de distintos programas de IV, los animales se ajustaban bastante bien a esa relación lineal, de manera que si en la alternativa a se ofrecía una mayor frecuencia de reforzamiento que en la alternativa b, los animales elegían más la alternativa a que la b y en proporción semejante a la tasa de reforzamiento obtenida en ambas alternativas, y al contrario si la alternativa a ofrecía una menor frecuencia de reforzamiento que la alternativa b.
Además de igualar la tasa relativa de respuesta con la tasa relativa de reforzamiento, como demostró Herrnstein, se ha observado que los animales igualan la tasa relativa de respuesta con otros parámetros que definen al reforzador, como pueden ser la magnitud del reforzador o su inmediatez. De esta manera se puede extender la formulación de la ley de igualación para incluir todos estos parámetros de reforzamiento siguiendo la Ecuación 5.2:
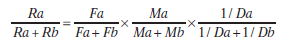
donde Ra y Rb se corresponden con las tasas de respuesta en las alternativas a y b; Fa y Fb con las tasas de reforzamiento en las alternativas a y b; Ma y Mb con las magnitudes de reforzamiento de las alternativas a y b; y Da y Db con las demoras al reforzador en las alternativas a y b. Nótese que en el caso de la demora del reforzador los valores se corresponden con la inversa del valor de la demora, pues los reforzadores son más preferidos cuanto más inmediatos (menos demorados).
La Ecuación 5.2 establece que todos los factores de reforzamiento influyen de forma igual en la elección, y en concreto de forma multiplicativa, de manera que cualquiera de esos factores (frecuencia, magnitud, demora) puede reducir la elección por una alternativa de respuesta aunque los otros factores sean altamente favorables.
Lo esencial de la ley de igualación es que establece una igualdad entre la tasa relativa de respuesta y la tasa relativa de reforzamiento (o cantidad relativa de reforzamiento, o demora relativa al reforzador), de manera que la proporción entre las respuestas emitidas en las alternativas debe ser igual a la proporción de los reforzadores obtenidos en dichas alternativas. En la ley de igualación no se equiparan tasas absolutas de respuesta y de reforzamiento, exclusivamente tasas relativas de respuesta y de reforzamiento.
Maximización: elección entre programas concurrentes de razón
Cuando se tiene que elegir entre dos alternativas de respuesta que proporcionan reforzadores de acuerdo a programas de razón diferentes (un programa concurrente RF-RF o uno RV-RV), los sujetos tienden a elegir la alternativa de respuesta que tiene una razón más baja, describiéndose dicho resultado como maximización. La maximización es un comportamiento adaptativo pues no tiene mucha ventaja dedicar esfuerzo a responder en una alternativa menos favorable a expensas de perder oportunidad de reforzamiento en la más ventajosa (en los de intervalo no ocurre, puesto que probando con la menos ventajosa también se pueden recoger reforzadores si ha pasado el tiempo estipulado). La maximización, que implica elegir en exclusiva la alternativa más favorable, no contradice, sin embargo, la ley de igualación. Es más, es el único comportamiento que en una situación de programa concurrente de razón cumple con la ley de igualación.
Por ejemplo, en un programa concurrente RV10 RV-20, si se responde en exclusiva al RV-10 (esto es, se maximiza), se obtendrán todos los reforzadores de dicho programa. La tasa de respuesta en RV-10 será igual a la tasa total de respuesta en las dos alternativas (porque no se dan respuestas en RV20) y la tasa relativa de respuesta será igual a 1, lo mismo que va a ocurrir con la tasa de reforzamiento total y la tasa relativa de reforzamiento en RV-10, que será 1 también. Como se puede apreciar la tasa relativa de respuesta es igual a la tasa relativa de reforzamiento, tal como estipula la ley de igualación.
También se han utilizado combinaciones de programa de intervalo con programas de razón, por ejemplo RV- IV. Lo óptimo sería que los animales se dedicasen casi en exclusiva al programa de razón, probando esporádicamente el de intervalo. Aunque en general se prefiere responder a la alternativa del programa de razón, la preferencia no es tan marcada como podría pensarse de haber habido una explotación óptima de los recursos, perdiendo más reforzadores de los necesarios por una dedicación extra al programa de intervalo (esto tiene importantes implicaciones teóricas, se verá más adelante)
Igualación temporal
Se ha demostrado experimentalmente que los organismos no sólo igualan la tasa relativa de respuesta con la tasa relativa de reforzamiento, sino que al mismo tiempo igualan el tiempo de estancia en las alternativas de respuesta con la tasa relativa de reforzamiento en dichas alternativas de respuesta. Para ello se ha utilizado una variante de programa concurrente, ideada por Findley. Consiste en presentar en una única tecla de respuesta los dos programas de IV en sucesión, cada uno señalado por una clave discriminativa distinta, como en un programa múltiple. Sin embargo, los sujetos pueden cambiar de programa de reforzamiento respondiendo en una segunda tecla, denominada de cambio. La gran ventaja del programa concurrente de Findley es que separa la respuesta de cambio de la respuesta instrumental, permitiendo comparar entre diversas respuestas instrumentales e incluso eliminar alguna de ellas.
Un ejemplo es el estudio de las preferencias de las palomas en varias fuentes de reforzamiento sin emplear respuestas instrumentales. Los picotazos en la tecla de cambio modificaban el color de la otra tecla, pero los animales no tenían que picotearla para obtener los reforzadores. Los reforzadores se administraron independientemente de la conducta de los sujetos a tasas diferentes dependiendo del color de la tecla. Lo único que podía hacer el animal era picotear la tecla de cambio para activar uno u otro programa de administración de la comida. Un primer picotazo tornaba la tecla de un color y activaba un programa de reforzamiento, un segundo picotazo cambiaba el color de la tecla y activaba el otro programa de reforzamiento, y así sucesivamente. La medida de preferencia en este estudio fue el tiempo de permanencia en los programas de reforzamiento, asumiéndose que una mayor permanencia reflejaría una mayor preferencia.
La igualación temporal es un hallazgo muy corriente en los experimentos de elección. Es posible encontrar igualación temporal con procedimientos concurrentes normales, así como con procedimientos concurrentes tipo Findley donde sea necesaria la respuesta instrumental, donde la respuesta instrumental no sea necesaria, e incluso donde la respuesta instrumental sea necesaria para un programa pero no para el otro. La igualación temporal se puede formalizar siguiendo la Ecuación 5.3:
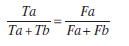
Siendo Ta y Tb los tiempos de permanencia en las alternativas a y b; y Fa y Fb las tasas de reforzamiento de dichas alternativas de respuesta.
Ley generalizada de la igualación
Al comienzo del Apartado 2 se ha hecho referencia a dos formas de medir la elección, los premios concurrentes y las respuestas instrumentales concurrentes, y también se ha hecho referencia a las limitaciones que presentaba el primero de estos métodos. El procedimiento de las respuestas instrumentales concurrentes supera las dificultades impuestas por el procedimiento de los premios concurrentes, pero, sin embargo, hay que considerar algunas influencias no deseables que intervienen en la elección de los sujetos entre respuestas instrumentales concurrentes. En primer lugar, cuando se tiene que elegir entre dos o más alternativas de respuesta se suele producir un tipo de comportamiento denominado de alternancia, caracterizado por el cambio intermitente de una alternativa de respuesta a otra sin que guarde relación con los reforzadores asociados a cada una de dichas alternativas de respuesta.
En las situaciones de la vida en libertad, los animales tienden a cambiar el lugar donde consiguen sus alimentos, y la alternancia es en este sentido un comportamiento reminiscente de esta tendencia natural de los animales. Además, en algunos programas de reforzamiento, principalmente los programas de intervalo, el animal puede ser reforzado por la primera respuesta que da después de pasar de una alternativa a otra. Este reforzamiento «accidental» puede fortalecer aún más el comportamiento natural de alternancia.
Dado que en las situaciones de elección en los laboratorios de psicología del aprendizaje interesa que el comportamiento de elección se guíe simplemente por las consecuencias de reforzamiento en las diferentes alternativas de respuesta, y no por otras variables, se tiene que controlar la influencia extraña que se introduce con este comportamiento alternante de los animales experimentales. Para ello los investigadores añaden la limitación de que no se refuerce la respuesta de cambio de alternativa por un tiempo. Este procedimiento se denomina demora por el cambio (DPC), y consiste en introducir un periodo temporal breve, de aproximadamente 2 ó 3 segundos, después de la primera respuesta a una de las alternativas para que pueda entrar en funcionamiento el programa de reforzamiento asociado a dicha alternativa de respuesta. En otras palabras, si los sujetos experimentales persisten en su comportamiento de alternancia, y se ha introducido la contingencia de DPC, no podrían obtener ningún reforzador en ninguna de las alternativas de respuesta. La consecuencia normal de haber introducido la contingencia de DPC es que los sujetos enfrentados con una situación de elección abandonan su comportamiento de alternancia y realizan la elección en base exclusivamente a las contingencias de reforzamiento asociadas con cada una de las alternativas de respuesta. Además de prevenir el reforzamiento inmediato de la conducta de alternancia, la DPC garantiza la independencia de los operandos de respuesta.
Existen muchas otras fuentes potenciales de influencias no deseables en los experimentos de elección, y genéricamente estas influencias se han denominado sesgos. Los sesgos pueden ser de muchos tipos, pero los más frecuentes en los experimentos de elección realizados en los laboratorios de conducta animal pueden ser, además de la conducta de alternancia descrita anteriormente, la disposición espacial de las alternativas de respuesta (izquierda frente a derecha), el color y la iluminación de dichas alternativas, o la fuerza requerida para responder en cada una de las alternativas. En un programa concurrente de reforzamiento se requiere que las alternativas de reforzamiento difieran exclusivamente en base a las características de reforzamiento, y que todos los demás factores permanezcan iguales. Baum (1974) ideó un método para corregir la influencia de los sesgos, por definición fuentes de influencia desconocida.
Partió de la idea conceptual de que los sesgos influyen en la elección de forma idéntica a los factores de reforzamiento (frecuencia, magnitud, demora), y formuló la ley generalizada de la igualación.
Para el caso de la frecuencia de reforzamiento (pero podría hacerse para cualquier otro factor de reforzamiento, o para todos juntos), la tasa relativa de respuesta se iguala a un factor multiplicativo de la tasa relativa de reforzamiento y de los sesgos relativos, y se puede expresar matemáticamente como se sigue por la Ecuación 5.4:
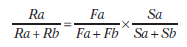
Donde Ra y Rb son las tasas de respuesta en las alternativas a y b respectivamente; Fa y Fb son las frecuencias (tasas) de reforzamiento en las alternativas a y b respectivamente; y Sa y Sb son los sesgos en las alternativas a y b respectivamente.
El método de Baum para corregir los sesgos consiste en tres pasos. En primer lugar, se deben equiparar los factores de reforzamiento entre las alternativas de respuesta. Por ejemplo, la frecuencia, magnitud y demora del reforzador deben ser iguales. En segundo lugar, se deben medir las preferencias relativas de los sujetos. Si los sujetos distribuyen las respuestas de forma igual entre las alternativas de respuesta, entonces no hay influencia de sesgos. Si, por el contrario, existe una desviación hacia una preferencia mayor por una de las alternativas, dicha elección indicaría la contribución de los sesgos, que se puede determinar cuantitativamente por el valor de la tasa relativa de respuesta. En tercer lugar, una vez conocido el valor de los sesgos relativos, se deben variar los factores de reforzamiento asociados con las alternativas de respuesta. Por ejemplo, se puede programar el doble de reforzamiento en una de las alternativas y comprobar si los sujetos eligen dicha alternativa el doble del valor de los sesgos relativos.
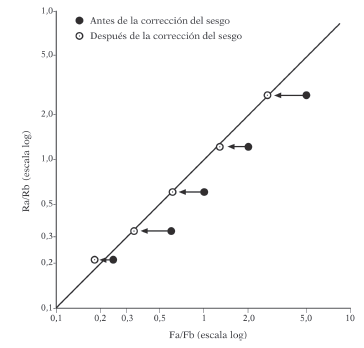
Si esto es así, a medida que se vayan variando los factores de reforzamiento entre las alternativas de respuesta se debería observar una desviación paralela a la igualación en la dirección del sesgo.Como la desviación producida por el sesgo es constante a cualquier valor relativo del reforzamiento, se puede corregir dicho valor en los resultados obtenidos. Gráficamente quedaría como en la Figura 5.6, donde se ve que el valor de los sesgos relativos se multiplica por cada valor de la tasa relativa de reforzamiento corrigiéndose el resultado sobre el eje de las abscisas.
Ya se ha visto que hay sesgos de respuesta que pueden incidir en la elección y que conviene corregir cuando no evitar (por imposible), aun así se parte de la situación ideal de que los animales (y nosotros) somos capaces de hacer cálculos exactos sobre las cualidades de los reforzadores y elegir proporcionalmente en consecuencia. Es considerar que el cálculo es puramente matemático, como si el cerebro, o las relaciones conducta-consecuencia, reflejasen una suerte de computación exacta. No es de extrañar que ajustes tan exactos como los predichos por la ley de igualación de Herrnstein en realidad no se cumplan y que las estimaciones en cuanto a las ventajas de reforzamiento de las alternativas de respuesta conduzcan a errores de estimación que es lo genuinamente psicológico. Ya se ha visto con anterioridad que la estimación del valor de un reforzador depende mucho de la experiencia previa o simultánea con otros reforzadores, de manera que el valor no es algo que provenga exclusiva mente de unos rasgos estrictamente objetivos sino que pueden ser relacionales, en comparación con otras alternativas o con experiencias previas. En el caso de los programas concurrentes sucede exactamente lo mismo. Es posible que la valoración de una de las alternativas de respuesta dependa no sólo de su valor objetivo, sino del valor que se ofrece en la otra alternativa. Y esto es así, habiéndose demostrado repetidamente.
A veces la alternativa de respuesta es sobrevalorada (si la otra alternativa es significativamente peor) y a veces es infravalorada (si la otra alternativa es manifiestamente mejor). Y este cálculo del valor de los reforzadores es la generalidad, lejos de la excepción. Existe sobreigualación cuando la mejor alternativa es valorada por encima de la preferencia establecida por la igualación perfecta; existe infraigualación cuando la mejor alternativa es valorada por debajo de la preferencia establecida por la igualación perfecta. Es más común encontrar infraigualación que sobreigualación, debido principalmente a la tendencia a cambiar de alternativa cuando se ha obtenido reforzamiento en una de ellas (el comportamiento de alternancia descrito anteriormente), lo que disminuye el ajuste perfecto a la igualación.
Cuando se habla de sobreigualación y de infraigualación, siempre se hace referencia a la tasa de respuesta en la alternativa más favorable (con mayor frecuencia de reforzamiento) en el contexto de las predicciones de la ley de igualación. Ello implica que las dos alternativas de respuesta no son iguales, siempre tiene que haber una más favorable. En estas circunstancias, la ley de igualación hace unas predicciones cuantitativas sobre las preferencias relativas de los sujetos basadas en la frecuencia relativa de reforzamiento.
En la Figura 5.7 se dibujan curvas hipotéticas de sobreigualación (curva de puntos) e infraigualación (curva de guiones), junto con la relación lineal de la igualación perfecta. Dado que los ejes son proporciones de respuesta y de reforzamiento entre las alternativas a y b, se debe entender que el valor de 1 se corresponde con la situación en que ambas alternativas de respuesta ofrezcan el mismo reforzamiento. En este caso, y si no hubiera sesgos, las respuestas se deberían distribuir por igual entre las dos alternativas.
Cuando la proporción de reforzamiento (Fa/Fb) sea mayor que 1, la alternativa a ofrecerá un mejor reforzamiento que la alternativa b. En este caso, si existiese sobreigualación se debería elegir la alternativa a proporcionalmente más de lo que se predice por la igualación perfecta. La proporción de respuestas (Ra/Rb) debería estar por encima de la igualación (curva de puntos en la parte derecha de la figura). Por el contrario, si existiese infraigualación se debería elegir la alternativa a proporcionalmente menos de lo que se predice por la igualación perfecta. Aquí la desviación de la igualación debería estar por debajo de la igualación (curva de guiones en la parte derecha de la figura).
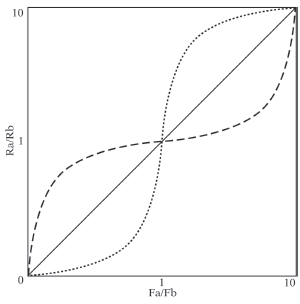
Lo más complejo es quizás entender la parte izquierda de la Figura 5.7, el caso en el que los valores de las tasas relativas de respuesta y de reforzamiento sean menores que 1. Lo más importante es darse cuenta que si la proporción de reforzamiento (Fa/Fb) es menor que 1, el programa b es mejor que el a (el denominador tiene que ser mayor que el numerador). La igualación predice que aquí b se debe elegir proporcionalmente más que a. Si existiese sobreigualación, dicha preferencia por b debería exagerarse en relación a lo predicho por la igualación perfecta. Al aumentar la proporción de respuestas en b sobre las de a, la tasa relativa de respuesta (Ra/Rb) debería disminuir. Eso es justamente lo que se representa por la curva de puntos en la parte izquierda de la figura. En el caso de infraigualación, por el contrario, el programa más favorable b se debería elegir en una proporción menor que la predicha por la igualación perfecta. La curva en este caso sería como la de los guiones en la parte izquierda de la figura, desviada por encima de la igualación.
Si volvemos por un momento a los resultados originales de Herrnstein representados en la Figura 5.5, ninguna de la palomas realmente se ajustó a la igualación perfecta, notándose que la paloma 231 (y quizás la 645) mostró sobreigualación y la paloma 055 infraigualación. Baum amplió la ley de igualación de Herrnstein para incorporar las desviaciones por sobreigualación o infraigualación, además de la influencia multiplicativa de los sesgos en la elección (como en la Ecuación 5.4), resultando en la Ecuación 5.5:
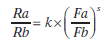
Siendo k la constante que representa los sesgos relativos (una constante calculada por el método explicado más arriba) y s un exponente que representa la sensibilidad hacia los programas de reforzamiento. Cuando k y s sean igual a 1, la ecuación se reduce a la de Herrnstein (con el cambio de que en los denominadores no se consideran el total de respuestas y de reforzamiento, sólo la tasa de respuesta y de reforzamiento de la alternativa b). Los valores de s inferiores a 1se corresponderían con la infraigualación, los valores de s superiores a 1 con la sobreigualación. La sobreigualación sería más frecuente cuando se utilice una contingencia de DPC relativamente larga o cuando resulte muy costoso el cambio de una a otra alternativa de respuesta. En el caso extremo en que s sea igual a 0, las tasas de respuesta en las alternativas a y b serán siempre las mismas independientemente de las tasas de reforzamiento que acompañen dichas alternativas de respuesta, reflejando una completa insensibilidad a las contingencias de reforzamiento.Esto podría ocurrir cuando los sujetos obtuviesen todos los reforzadores respondiendo simplemente a las dos alternativas de respuesta en estricta alternancia, o de acuerdo a cualquier otro patrón de comportamiento que fuese independiente de los valores de los programas de reforzamiento.
Teorías de igualación
Las ecuaciones de igualación vistas hasta ahora se refieren a relaciones entre variables de comportamiento, a cómo diferentes aspectos de la conducta se relacionan entre sí, estableciendo relaciones muy precisas entre aspectos del registro de la conducta como la tasa de respuesta y aspectos de los reforzadores que dependen de la propia ejecución operante, como puede ser la tasa de reforzamiento.
Ambas mediciones son reflejo de la ejecución operante, donde se requiere la emisión de una respuesta particular para la obtención del reforzador, pero los reforzadores no se pueden obtener sin una respuesta previa. Por tanto, las diferentes versiones de la ley de igualación lo que establecen son relaciones (correlaciones, si se quiere) entre al menos dos medidas de la conducta, que como tal son variables dependientes de la ejecución operante. La forma en que dos aspectos de la conducta se relacionan constituye una explicación meramente descriptiva, no presupone ninguna explicación mecanicista. La forma en que los animales llegan a la igualación puede ser variada y explicada, por tanto, a través de diferentes mecanismos.
Al igual que con los programas básicos de reforzamiento, en la igualación hay dos enfoques principales, la aproximación molecular y la aproximación de corte más molar, que tienen que explicar cómo se distribuyen las respuestas entre las alternativas disponibles asi como el momento en que se produce el cambio de una a otra alternativa.
La aproximación teórica molecular afirma que el cambio de una alternativa de respuesta a otra se realiza en el momento en que la probabilidad momentánea de reforzamiento sea mayor en la otra alternativa.Basa su análisis en el cálculo de las probabilidades relativas de reforzamiento en cada momento, de aquí que se denomine molecular.
La aproximación molar, de forma contraria a la teoría molecular, afirma que los animales distribuyen sus respuestas de acuerdo a un cálculo global de las tasas relativas de reforzamiento entre las dos alternativas de respuesta, eligiendo más aquella alternativa que proporciona una mayor tasa de reforzamiento. A través de un cálculo general, los animales ajustan proporcionalmente sus respuestas entre los reforzadores disponibles en las diferentes alternativas, cumpliendo la ley de igualación.
Aunque las predicciones de la teoría molecular, y el mecanismo propuesto, parecen demasiado precisas, justo en su precisión está la virtud, en el sentido de ser comprobable, y lo que se ha visto es que en general este mecanismo explica bastante bien la distribución de respuestas en programas concurrentes de intervalo, donde los animales podrían responder de muchas maneras pero lo hacen de forma muy aproximada a como predice la teoría. Además, la aproximación molar tiene problemas para explicar resultados como los comentados sobre la no preferencia casi exclusiva por el programa de razón cuando se presenta un programa concurrente RV-IV (Apartado 2.2). También tendría más dificultad que la aproximación molecular para explicar por qué los animales en general prefieren reforzadores variables a fijos cuando en ambos se ofrezca un promedio igual de tasa de reforzamiento.
Para la aproximación molecular, en la administración de reforzadores variables se aumenta la probabilidad de que haya una mayor contigüidad entre la respuesta y la consecución del reforzador. A favor de esta idea estaría el resultado de que habiendo una mayor preferencia por los reforzadores variados, sin embargo no existe tal preferencia por responder de forma variada frente a repetitiva si se mantienen los reforzadores fijos.
Una tercera teoría, denominada del mejoramiento, puede considerarse una síntesis de las aproximaciones molecular y molar. Según esta idea, los organismos eligen entre dos fuentes de premio de manera que se igualen las tasas locales de reforzamiento, respondiendo a la alternativa que en un momento dado presenta una mejor tasa local de reforzamiento.
La mejora se establece en términos de tasa local de reforzamiento, más que en términos de probabilidad momentánea de reforzamiento (como hacía la aproximación molecular). Así, los resultados tienen un alcance a más largo plazo que la teoría molecular, pero no se refiere a tasas globales de reforzamiento, como ocurre con la teoría molar. Intrínseco a la teoría del mejoramiento es la igualación temporal, puesto que los sujetos al elegir más la alternativa que proporcione un mejor reforzamiento, darán una mayor tasa de respuesta, obtendrán una mayor tasa de reforzamiento y permanecerán más tiempo en dicha alternativa de respuesta. Como resultado de todo ello las tasas locales de respuesta y de reforzamiento (el número de respuestas o de reforzadores por tiempo de estancia en la alternativa) serán iguales o muy parecidas entre las diferentes alternativas de respuesta, por cuanto se responderá menos a la alternativa menos favorable, se obtendrán menos reforzadores en ella, pero también se le dedicará menos tiempo.
Las tasas locales de respuesta y de reforzamiento, por tanto, serán iguales en las diferentes alternativas de respuesta, siendo esa la consecuencia de elegir en cada momento la alternativa que proporcione la mejor tasa local de reforzamiento. La teoría de la mejora se deriva perfectamente de la igualación: teniendo en cuenta el tiempo empleado en responder a cada alternativa (como veíamos anteriormente en relación con la igualación temporal – Ecuación 5.3.), se puede derivar con cierta lógica (y matemáticamente) que los animales al igualar están realmente equiparando las tasas locales de respuesta y de reforzamiento entre las alternativas de respuesta.
Impulsividad y autocontrol: la elección con compromiso
En cuanto a la medida de la elección, existe un último procedimiento experimental que introduce ventajas sobre el procedimiento de las respuestas instrumentales concurrentes, que es el hasta ahora referido para el estudio de la elección. Este procedimiento se denomina cadenas concurrentes de respuesta, y con él no se mide la elección entre premios de forma directa, ni tampoco se mide directamente la elección entre respuestas instrumentales concurrentes, sino que se mide la elección entre diferentes fuentes de premio.
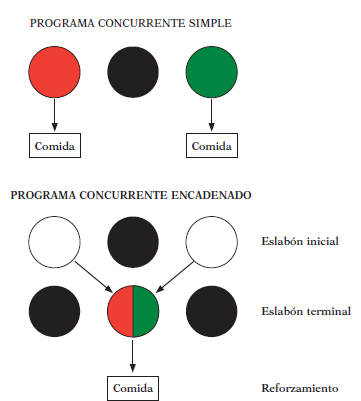
En la figura se representa un esquema de un programa concurrente simple (como los tratados hasta ahora en este capítulo) y otro de un programa concurrente encadenado. En el programa concurrente simple (arriba) se da a elegir a los animales entre dos alternativas de respuesta (en este caso, rojo frente a verde), cada una acompañada de un programa de reforzamiento (comida) particular. El programa concurrente encadenado (abajo), contrario al simple, se compone como mínimo de dos pasos, un eslabón inicial donde el sujeto tiene que elegir entre dos alternativas de respuesta idénticas (blanco frente a blanco), y un eslabón terminal donde se proporcionan los reforzadores por responder en la alternativa de respuesta elegida durante el eslabón inicial.
Si se hubiese elegido la alternativa de la izquierda, la tecla central se iluminaría de rojo y se acompañaría de un programa de reforzamiento particular; si se hubiese elegido la alternativa de la derecha, la tecla central se iluminaría de verde y se acompañaría de otro programa de reforzamiento. Una vez transcurrido un tiempo predeterminado en el eslabón terminal, se vuelve a presentar el eslabón inicial hasta que el sujeto elija otra vez una de las alternativas de respuesta y se vuelva a pasar al eslabón terminal. Este procedimiento para medir la elección permite, entre otras cosas, que los sujetos sean más consecuentes al decidir sus respuestas de elección en comparación con los otros procedimientos experimentales de elección discutidos anteriormente. Este procedimiento también permite separar el aprendizaje de responder para conseguir el reforzador en los eslabones terminales, del aprendizaje de elección en el eslabón inicial. Es, por tanto, un procedimiento más limpio para medir la elección, descontaminada de los propios efectos del reforzamiento sobre la tasa de respuesta (que se podrían confundir con respuestas de elección).
Al ser sometidos a programas concurrentes encadenados, los sujetos experimentales normalmente igualan la tasa relativa de respuesta en los eslabones terminales con la tasa relativa de reforzamiento en dichos eslabones terminales (el resultado normal de la igualación), pero también igualan la tasa relativa de respuesta en el eslabón inicial con la tasa relativa de reforzamiento en los eslabones terminales. Los programas concurrentes encadenados se asemejan más a las elecciones en la vida cotidiana, donde optar por una alternativa te compromete por un tiempo hasta poder cambiar de opción y donde normalmente no se puede estar cambiando caprichosamente de alternativa en cada momento. Por ejemplo, al inicio de un curso académico un estudiante decide matricularse de un cierto número de asignaturas, para darse cuenta inmediatamente de que la elección de alguna de ellas mejor la hubiese dejado para otro momento, pero el cambio de matrícula de asignatura no puede realizarse siempre, sólo cuando se habilite su disponibilidad, mientras tanto se ha adquirido un compromiso de permanencia. Igual se puede aplicar para elecciones de ir a ver una película u otra en una sala multicines, o elegir un plato de un menú en lugar de otro.
Rachlin y Green realizaron un trabajo seminal que ilustra perfectamente las implicaciones diferenciales de utilizar un programa concurrente simple o uno encadenado cuando dieron a elegir a sus animales entre una opción que implicaba una recompensa pequeña inmediata y otra que implicaba una recompensa mayor demorada. Cuando la elección era directa, como en el caso del programa concurrente simple, se prefería la opción que llevaba al premio pequeño inmediato aun cuando dicha opción no fuese la más ventajosa en términos de obtención del máximo reforzamiento. La situación estaba diseñada para que por esperar al premio mayor en la otra opción de respuesta se conseguía a la larga un mejor reforzamiento. Era como si la inmediatez del reforzador influyese más en la elección que la magnitud. Cuando utilizaron un programa concurrente encadenado e introdujeron un tiempo constante de espera para poder acceder a la oportunidad de que las respuestas fuesen reforzadas (por la introducción del eslabón inicial de elección), las preferencias cambiaron y ahora los animales optaron más por la alternativa que llevaba al reforzador mayor pero más demorado. Al introducir una pequeña demora entre la elección y la respuesta reforzada, la fuerza de la inmediatez del reforzador se debilitó y la elección se guió más por la magnitud del reforzador. La preferencia por una recompensa pequeña inmediata se denomina impulsividad; la preferencia por una recompensa mayor demorada se denomina autocontrol. El trabajo de Rachlin y Green muestra que demorar un poco la entrega del reforzador pequeño hace que su fuerza se debilite y se prefiera esperar (ya que hay que esperar) a uno de mayor magnitud.
Estudios como estos de autocontrol muestran que en realidad los pesos relativos de los diferentes factores que definen a los reforzadores no influyen de la misma manera en la elección, y que por tanto la Ecuación 5.2 no es del todo correcta. La idea expresada en la ecuación sigue siendo válida (como se ha visto a lo largo de todo este apartado) pero no que cada uno de los factores tenga que influir de la misma forma en la distribución de las respuestas entre las alternativas de elección, no al menos en el caso de la magnitud y de la demora al reforzador. Una forma de explicar los resultados de los estudios de autocontrol a través de la ley de igualación es aceptar una extensión de la ley generalizada de la igualación (Ecuación 5.5) que incorpore los parámetros de frecuencia (inmediatez) y magnitud del reforzador como se detalla en la Ecuación 5.6:
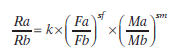
Donde los exponentes de la sensibilidad (s) a las características de los reforzadores se hacen diferentes para la frecuencia (sf) y para la magnitud (sm).
La noción del valor de los reforzadores
Una aproximación complementaria a la de la ley de igualación es integrar los distintos factores de reforzamiento bajo el concepto de valor de la alternativa, y esto se ha investigado de forma bastante sistemática con los parámetros de la magnitud y la demora del reforzador (como en los estudios de autocontrol comentados en el apartado anterior, pero también con programas no concurrentes). El valor de una alternativa de respuesta aumentará con la magnitud del reforzador y disminuirá con la demora para la entrega del reforzador. Matemáticamente el valor del reforzador vendrá determinado, en este caso, por el cociente magnitud/demora.
Este análisis simple nos permite predecir algunos fenómenos interesantes, algunos de ellos relativamente complejos en apariencia. Imaginemos una situación donde se ofrece un programa concurrente de IV 30-seg IV 20-seg, pero el reforzador es el doble en el primer componente. En esta situación, los sujetos elegirán la alternativa de mayor premio más demorado, esto es, mostrarán un comportamiento autocontrolado. Esto es así porque el valor de la alternativa IV 30-seg es 2/30 = 0,07 (dos reforzadores cada 30 seg por término medio), mientras que el valor de la alternativa IV 20-seg es 1/20 = 0,05 (un reforzador cada 20 seg por término medio).
Tomemos otro ejemplo, un programa concurrente IV 40-seg IV 15-seg, con el doble de cantidad de reforzador en el primer componente. En este caso, los animales elegirán más la opción de IV 15-seg (1/15 = 0,07) que la opción de IV 40-seg (2/40 = 0,05). Esto representaría un caso de impulsividad.
Aunque los casos anteriores se han puesto como ejemplos de autocontrol e impulsividad, la verdad es que no son del todo correctos. En cualquiera de las dos situaciones, siempre había una alternativa que ofrecía una mejor frecuencia de reforzamiento, lo que es plenamente acorde con la ley de igualación. Para entender mejor cómo funciona el autocontrol es necesario partir de una situación donde los animales elijan la alternativa que les ofrezca un premio menor más inmediato. Por ejemplo, en un programa concurrente IV 5-seg IV 10-seg que suministre 1,5 veces más cantidad de reforzador en el segundo componente, los sujetos elegirán con más probabilidad el programa IV 5-seg (1/5 = 0,2) que el programa IV 10-seg (1,5/10 = 0,15). Si se añadiera un retraso constante a la entrega de las dos recompensas, como en los programas concurrentes encadenados, se podrían invertir las preferencias. Por ejemplo, añadiendo un intervalo temporal de 20 seg a las dos alternativas, el valor de la alternativa IV 5-seg sería 1/25 = 0,04, y el valor de la alternativa IV 10-seg sería 1,5/30 = 0,05. Añadir un retraso constante a la entrega de los dos reforzadores vuelve un comportamiento “impulsivo” en “autocontrolado”, y esto es precisamente lo que demostraron Rachlin y Green.
Mazur ha propuesto que el cambio de un comportamiento impulsivo a uno autocontrolado se puede explicar mediante una función hiperbólica que podría expresarse como sigue (Ecuación 5.7):
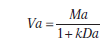
Donde Va sería el valor de un reforzador a que tuviese una magnitud Ma y una demora Da; k sería una constante que representa la tasa de descuento de la demora para cada individuo particular en una situación dada (una tasa que indica hasta qué punto son apreciados los reforzadores demorados).
El valor del reforzador sería mayor a medida que su magnitud fuese mayor y la demora para su obtención menor, pero la relación no sería lineal sino hiperbólica. Por ejemplo, para una magnitud dada, el valor del reforzador aumentaría en una proporción creciente a medida que sea menor la demora. En el caso de reforzamiento inmediato, el valor del reforzador vendría exclusivamente determinado por su magnitud.Aplicando esta ecuación se puede comprobar que cuando un reforzador grande y otro pequeño son demorados, aunque el primero lo sea más que el segundo, el valor del reforzador grande será superior al del pequeño (autocontrol). El valor del reforzador pequeño será mayor que el del grande, por el contrario, cuando la espera para el primero sea relativamente pequeña (impulsividad).
El valor aversivo de un castigo también cambia mediante una función hiperbólica semejante a la de la recompensa y expresada en la Ecuación 5.7. Como en el caso del reforzamiento, en la determinación del valor aversivo relativo de dos castigos de intensidad y demoras diferentes, tiende a incidir más la diferencia entre sus intensidades que entre sus demoras si se trata de castigos muy diferidos (aquí se «preferiría» el castigo pequeño), pero tiende a incidir más la diferencia entre sus demoras que entre sus intensidades cuando el menos intenso es relativamente inmediato (aquí se «preferiría» el castigo grande).
La tasa de respuesta en relación a la ley de igualación
Herrnstein amplió la ley de igualación al considerar que cualquier situación implica necesariamente una elección, incluso cuando sólo se ofrezca una alternativa de respuesta, como en los programas básicos de reforzamiento. En este caso, los animales deben elegir entre responder y no hacerlo. Mejor dicho, los animales están confrontados entre responder de la manera específica que requiere el experimentador (por ejemplo, presionar una palanca o picar una tecla) y realizar otras actividades (asearse, dar vueltas, picotear el suelo, oler agujeros de la cámara experimental). Los sujetos recibirían reforzadores explícitos, programados por la ocurrencia de la respuesta operante explícita, pero también recompensas implícitas por las otras actividades que pueden realizar. Por tanto, tiene que considerarse que el reforzamiento total de la situación comprende los reforzadores programados y los reforzadores no explícitamente programados. Matemáticamente se puede describir esta conducta de elección como en la Ecuación 5.8:
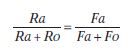
Donde Ra representa la tasa de respuesta operante específica del programa, Ro la tasa de las otras actividades del animal, Fa la frecuencia de reforzamiento explícito programado, y Fo la frecuencia de reforzamiento intrínseco de las otras actividades.
Es más, Herrnstein teorizó que la tasa total de conducta (Ra + Ro) debería ser una constante pues, en general, se debe aceptar la idea de que los organismos siempre están haciendo algo, que siempre están desarrollando alguna actividad (aunque sea descansar). Por tanto, la suma de la tasa de respuesta criterio más la de cualquier otra actividad debe ser siempre igual. Si la tasa de respuesta criterio bajase, necesariamente quiere decir que los animales estarían dedicándose a otras actividades; si subiese, las otras actividades disminuirían. Es decir, la adquisición de una respuesta particular implica una redistribución de respuestas entre las alternativas disponibles. Si se representa la constante del total de la tasa de respuesta por el parámetro k (Ra + Ro = k), despejando Ra en la Ecuación 5.8 quedaría como sigue (Ecuación 5.9):
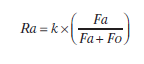
Lo que significa que la tasa absoluta de una conducta (Ra) está en función de la tasa relativa de reforzamiento de esa conducta en relación con otras. Una forma de aumentar la tasa de la respuesta sería aumentar la tasa de reforzamiento asociada a esa conducta (haciendo que Fa fuese mayor), y otra sería disminuir la tasa de reforzamiento alternativo (haciendo que Fo disminuyese). Esta ecuación es a menudo referida como la cuantificación de la ley del efecto de Thorndike en la medida en que especifica cuantitativamente cómo las consecuencias afectan a la conducta, y transforma una ley de igualación puramente descriptiva en una teoría.