Tradicionalmente se pensaba que lo más importante para un buen condicionamiento, y obtención por tanto de la RC esperada, era el emparejamiento repetido de la asociación EC-EI. Aunque esto es imprescindible, no es suficiente para un buen condicionamiento: también se debe cumplir que el EC sea un buen predictor del EI.
El concepto de contingencia
Rescorla descubrió que el mero emparejamiento EC-EI no siempre da lugar a condicionamiento. Para medir el grado en que una clave o estímulo, el EC, es un buen predictor de la aparición de otro, el EI, se utiliza el concepto de contingencia.
Las posibles alternativas de emparejamiento EC-EI en un ensayo de condicionamiento concreto no se limitan a la aparición de ambos; en fenómenos de extinción por ejemplo, la aparición del EC va seguida de la no aparición del EI, lo que aporta una gran información a pesar de que no se da contigüidad entre ambos estímulos. Estas posibles alterativas, se resumen en una tabla de contingencias de matriz 2x2 que representa las ocurrencias conjuntas del EC y el EI con sus cuatro posibles combinaciones:
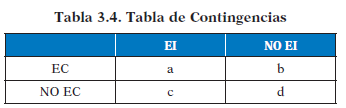
- indica el número de ensayos de condicionamiento en los que habiendo aparecido el EC después aparece el EI
- indica el número de ensayos de condicionamiento en los que habiendo aparecido el EC después no aparece el EI
- indica el número de ensayos de condicionamiento en los que no habiendo aparecido el EC después si aparece el EI
- indica el número de ensayos de condicionamiento en los que ninguno de los dos estímulos aparece.
Sabiendo esto, se pueden calcular probabilidades condicionales, teniendo en cuenta toda la info obtenida de las cuatro celdas, o una info relativa por fila o por columna.
Por ejemplo la probabilidad de que se dé el EI después del EC (denominada P 1 ) se calcula teniendo en cuenta las veces que el EI aparece después de que lo haga el EC en función de todas las veces, en total, que ha aparecido el EC:
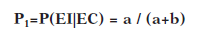
De la misma forma podemos hacer el cálculo relativo de la probabilidad de que el EI tenga lugar tras la NO aparición del EC (P0) teniendo en cuenta todos los casos que no ha aparecido EC (haya o no haya aparecido después el EI):
P0 = P (EI | noEC) = c/(c+d)
Estas son las dos fórmulas utilizadas para el cálculo de la contingencia en aprendizaje asociativo.
La contingencia se calcula teniendo en cuenta la probabilidad de la aparición del EI en presencia del EC en relación a la aparición del EI sin que previamente haya aparecido el EC. El índice resultante de este cálculo de contingencia se llama ΔP y puede comprender valores entre -1 y 1
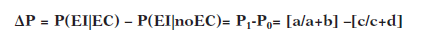
Según sus valores hay tres tipos de contingencia:
Contingencia positiva: si la aparición del EC es un buen predictor del EI, el EI debe ocurrir con más probabilidad cuando el EC ha sido presentado previamente que en ausencia de este. En este caso se da un condicionamiento excitatorio
P(EI | EC) > P(EI | noEC) es decir P1 > P0
ΔP > 0
En el caso de que el EI sólo ocurra en presencia del EC y nunca en su ausencia, la contingencia será perfecta:
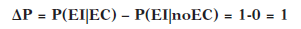
Contingencia nula: Si la probabilidad de que el EI apareciese en presencia o ausencia del C fuese la misma, la contingencia tendría un valor numérico de 0. Esto implica, en teoría, una ausencia total de condicionamiento.
P(EI | EC) = P(EI | noEC) es decir P1 = P0
ΔP = 0
Aunque en teoría debería darse una falta de condicionamiento, en la práctica tiene lugar el efecto de irrelevancia aprendida: el sujeto aprende que no hay una relación entre EC y EI lo que retrasa un posterior aprendizaje de dicha relación. Es similar al fenómeno de preexposición.
Contingencia negativa: indica que el EC es un gran predictor de ausencia del EI, pero no de su presencia. Esto implica que el EI es menos probable en presencia del EC, lo que hace que éste último sirva como predictor de la NO aparición.
P(EI | EC) < P(EI | noEC) es decir P1 < P0
ΔP < 0
En el caso de que el EI siempre apareciese en ausencia del EC y nunca en su presencia:
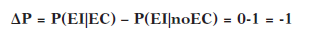
Cuando la contingencia es negativa el condicionamiento es inhibitorio: un EC predice la no aparición del EI. El Ei aparece con más frecuencia cuando el EC no está presente.
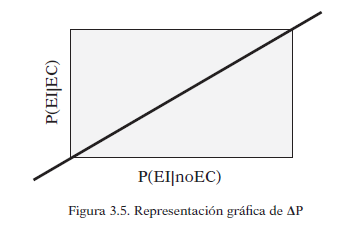
La contingencia se puede representar gráficamente, los valores superiores a la diagonal representan la contingencia positiva (triángulo superior izquierdo) mientas que los que están por debajo, representan contingencia negativa (triángulo inferior derecho). La diagonal sería ausencia de condicionamiento, es decir contingencia nula: ΔP=0
Fenomenos de competición de claves
Puede ocurrir que se dé una contingencia perfecta entre EC y EI (es decir, que el EC sea un buen predictor del EI) y aún así la RC no tenga lugar. Esto es lo que muestran los fenómenos de competición de claves. En estos fenómenos se da una competición entre los distintos ECs presentes para ser el mejor predictor del EI.
Incluso cuando la contingencia entre cada uno de ellos y el EI es perfecta, existen otros factores que pueden influir en el condicionamiento, favoreciéndolo o dificultándolo. Hay varios factores, pero destacan el ensombrecimiento y el bloqueo.
Ensombrecimiento
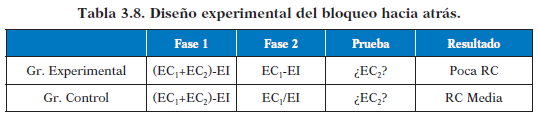
En este efecto son dos los ECs presentes de forma simultánea. Por ejemplo una luz (EC1) y un sonido (EC2) que queremos condicionar con una descarga posterior (EI) para provocar una respuesta de miedo. Aunque la contingencia entre EC1 y EI, y entre EC2 y EI es perfecta, ambos ECs van a competir para ser un mejor predictor del EI. Por eso al aparecer juntos, EC2 ensombrece a EC1, teniendo como consecuencia una menor RC frente a EC1 con respecto a ese mismo EC en un grupo de control en el que no ha tenido lugar el ensombrecimiento. Aquí se muestra el diseño experimental:
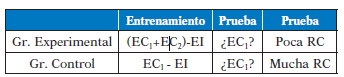
Ejemplo : he comido huevos fritos con patatas, y horas después me siento mal. En vez de pensar que ambos me han sentado mal, creo que han sido los huevos fritos los responsables del malestar estomacal.
Este efecto puede revertirse si se lleva a cabo una recuperación del ensombrecimiento. Para ello, tras el ensombrecimiento, debemos mostrarle al sujeto que ahora el estímulo ensombrecedor ya no es un buen predictor del EI, con lo que conseguimos que la RC frente al EC ensombrecido aumente.

Bloqueo
El bloqueo es un efecto que consta de dos fases de entrenamiento. La aparición conjunta de dos ECs igualmente contingentes con el EI determina la RC frente a cada uno de ellos.
En este caso el emparejamiento previo (en la primera fase) de un EC1 con el EI correspondiente, determinará el condicionamiento de un EC2 posterior con el mismo EI, cuando ambos ECs aparecen juntos.Es decir inicialmente se asocia EC1-EI y cuándo este está completamente condicionado se añade el segundo EC2. La poca fuerza de la RC ante el EC2 en la fase de prueba muestra que el aprendizaje previo del EC1 bloquea el desarrollo de la RC ante el EC2 añadido en la segunda fase.
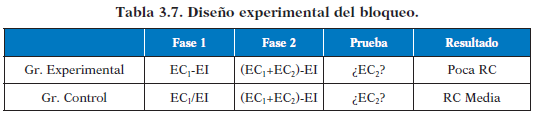
Ejemplo: cada vez que como huevos fritos siendo malestar estomacal. Ayer mi madre me puso huevos fritos con patatas para comer. Como ya he sufrido el malestar comiendo solo huevos, si como patatas sin huevos no me producirá por si solas el malestar.
Experimento: una luz EC1 la condicionamos con una descarga EI para provocar una respuesta de miedo en animales. En la segunda fase añadimos un EC2, por ejemplo un sonido. Aunque la contingencia entre el sonido y la descarga sea perfecta, el hecho de que la luz (EC1) se haya mostrado como predictor eficaz, va a dar como resultado una menor RC ante el EC2 si lo comparamos con un grupo de control en el que no hemos establecido la asociación EC1-EI.
Hay que controlar muy bien que los grupos experimental y de control sean lo más parecidos metodológicamente hablando, por ello se presentan los estímulos el mismo número de veces en ambos grupos, pero en el caso del grupo control se presentan explícitamente desemparejados el EC1 y el EI para que no se cree asociación alguna.
Si invertimos las fases de entrenamiento en un diseño de bloqueo, da lugar al bloque hacía atrás: primero entrenamos el compuesto de ambos ECs seguidos por el EI
Teorías del aprendizaje
Modelo Rescorla-Wagner
La primera vez que se asocia un EC con un EI resulta sorprendente, puesto que hasta el momento el EI no era predicho por ningún elemento, y por ello, aprendemos algo nuevo sobre la asociación EC-EI. El emparejamiento sucesivo, a lo largo del entrenamiento, hace que nos resulte menos sorprendente la aparición del EI a continuación del EC. En algún momento, el EC predice de forma perfecta al EI, lo esperamos sin duda después del EC, por lo que el EI no sorprende de ninguna manera y el aumento en el aprendizaje no tiene lugar ya.
Debido a la importancia del concepto de sorpresividad en el proceso de aprendizaje, Rescorla y Wagner propusieron un modelo asociativo para que aprendizaje que sigue siendo una referencia. La principal característica es que asume que en un ensayo de condicionamiento el aprendizaje sólo tiene lugar si el EI es sorprendente.
Sugieren que la fuerza asociativa entre un EC y un EI aumenta en cada ensayo, hasta que el EC predice completamente el EI y éste deja de ser sorprendente, punto en el cual dicha fuerza alcanza su máximo posible. Estas variaciones de la fuerza asociativa en cada ensayo dependen de:
- La saliencia del EC y el EI (que llamaremos α y β), constantes durante todo el proceso de aprendizaje. Numéricamente, se puede expresar entre un mínimo de 0 y máximo de 1, para ambos estímulos en caso de que estén presentes. Habitualmente la saliencia del EC toma un valor de 0,5 y la del EI de 1.
- La magnitud del EI (λ, lambda). Tras el EC en un ensayo de condicionamiento, puede tener lugar la aparición del EI, en cuyo caso el valor de λ sería 1, o no tener lugar en cuyo caso el valor sería 0. El nivel máximo de esperabilidad del EI (asíntota) correspondería a un λ=1
- La fuerza asociativa que la asociación EC-EI ha adquirido hasta el ensayo anterior de condicionamiento (Vn-1). Indica el aprendizaje previo sobre la relación EC-EI llevado a cabo hasta ese momento. Su valor puede oscilar entre 0 y 1.
El cálculo final del incremento de la fuerza asociativa entre el EC y el EI en un ensayo concreto (n) de aprendizaje se calcula con la siguiente formula:
ΔVn = αβ(λ - Vn-1)
Este incremento de la fuerza asociativa en un determinado aprendizaje ( ΔV n ) es directamente proporcional a la saliencia de ambos estímulos (α y β) y depende de la diferencia entre el máximo de aprendizaje adquirible (λ) y la fuerza de la asociación hasta el ensayo anterior (Vn-1). ΔV puede oscilar, dependiendo de las condiciones, entre valores de -1 a 1.
En esta fórmula el término (λ-Vn-1) denota la sorpresividad del EI. Porque λ indica si el EI está presente y en qué magnitud, y Vn-1 se refiere al término del aprendizaje, describe en qué medida el EC predice el EI.La diferencia entre los términos es la diferencia entre lo que podemos llegar a aprender sobre la asociación EC-Ei y lo que hemos aprendido hasta ahora: es decir lo sorprendente que resulta la aparición del EI.
Cuanto mayor sea Vn-1 el EC se convierte en un mejor predictor del EI, y la diferencia (λ-Vn-1) va siendo cada vez menor, hasta que no ocurren más cambios.
La fuerza asociativa neta (V) en un ensayo determinado se calcula sumando la fuerza asociativa adquirida en el entrenamiento hasta el ensayo anterior, y el incremento de la misma en el ensayo actual.
V = Vn-1 + ΔVn
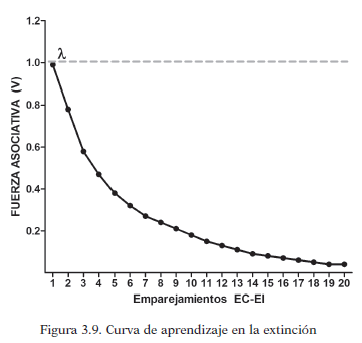
En la siguiente figura se muestra el crecimiento de la fuerza asociativa que se crea entre EC-EI a medida que se repiten los emparejamientos en el tiempo de estos estímulos, lo que es denominado “curva de aprendizaje”.
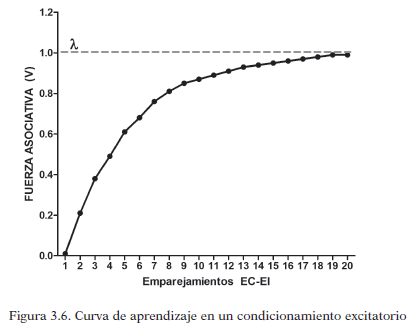
En cada ensayo hay aumento de la fuerza asociativa, por tanto se da aprendizaje. En los primeros ensayos, ese crecimiento es mayor, y va disminuyendo según avanza el entrenamiento, según los autores, ocurre porque el EI es cada vez menos sorprendente. Por eso en los primeros ensayos el paréntesis (λ-V n-1) tiene valores mayores. Dicho incremento del aprendizaje, al igual que la sorpresividad, van disminuyendo hasta que llega a una asíntonta, es decir, el aumento del aprendizaje es cercano a 0 y la fuerza asociativa de la asociación alcanza el 100% de su valor.
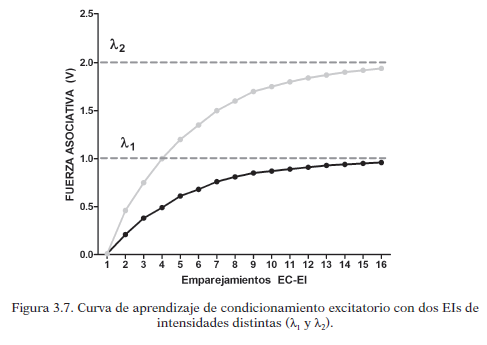
La sorpresividad del EI depende directamente de la magnitud o intensidad del mismo (λ) lo que influye en el aprendizaje. El comportamiento de la curva de aprendizaje en referencia a la utilización de diferentes magnitudes se ve en la siguiente gráfica: utilizar dos magnitudes distintas de un EI da lugar a curvas de aprendizaje que se comportan distintas. Cuando la intensidad es mayor, λ es mayor y más alta es la asíntota que puede alcanzar el aprendizaje.
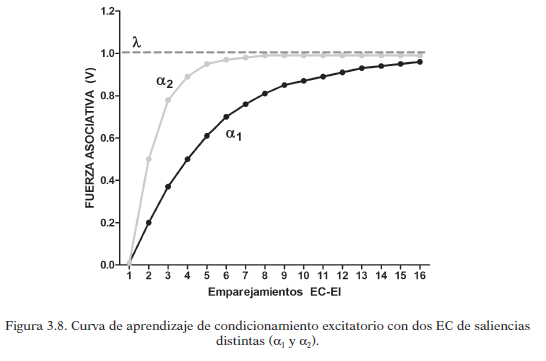
La saliencia del EC (α) puede modificar la cantidad de aprendizaje de un ensayo, ya que se multiplica por el factor de sorpresividad: cuanto mayor sea la saliencia del EC mayor será el aprendizaje en ese ensayo. Una mayor saliencia hace que se alcance más rápido la asíntota del aprendizaje, aunque no afecta al propio máximo del aprendizaje que viene determinado por la magnitud del EI.
En los efectos de competición de claves, como el bloqueo o el ensombrecimiento, al estar presentes varios estímulos, la capacidad predictiva del EC se ve afectada por la presencia de los mismos. Según Rescorla y Wagner si dos ECs se presentan en compuesto, ambos contribuyen a predecir el EI y por lo tanto influyen en los cambios de la fuerza asociativa en dicho ensayo de condicionamiento. Para tener en cuenta esto, modificaron su fórmula básica sustituyendo Vn-1 por ΣV n-1:
ΔV = αβ(λ - ΣVn-1)
ΣV n-1 indica la suma de todos los valores de Vn-1 de todos los estímulos presentes en este ensayo. De esta forma el valor de sorpresa viene dado por la diferencia entre λ y la suma del valor asociativo de todos los estímulos presentes. Además de la adquisición, esta teoría puede dar explicación a otros fenómenos del aprendizaje asociativo como la competición de claves, la extinción o el condicionamiento inhibitorio.
Bloqueo
Como ya se ha dicho, este efecto se da porque la asociación entre un nuevo EC y el EI se ve alterada por dicho EI ya era predicho de manera efectiva por otro EC
Segñun Rescorla y Wagner, la primera fase de condicionamiento de un bloqueo, cuando el animal está aprendiendo la asociación entre EC1 y EI, dicho EC adquiere un valor de V positivo a medida que transcurren los ensayos hasta llegar a la asíntota del aprendizaje. Suponiendo que utilizásemos un EI que tuviese un λ=1, al final de la primera fase de condicionamiento, el valor asociativo V ECI sería cercano a 1.
En el primer ensayo:
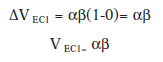
En el último ensayo:
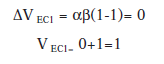
En el último ensayo la fuerza asociativa del EC1 ha llegado a su valor asintótico y por lo tanto prácticamente no se da incremento de la misma en dicho ensayo.
Durante la segunda fase de entrenamiento, los ensayos de condicionamiento continúan, pero se añade el EC2 al EC1, ambos seguidos del EI. Así que para calcular la fuerza asociativa entre ese nuevo EC2 y el EI, la V de la ecuación se convierte en ΣV n-1 , que muestra la fuerza asociativa de todos los estímulos presentes en el ensayo, tanto del EC1 como del EC2, y su influencia sobre el incremento del aprendizaje:
ΔVEC2 = αβ(λ - ΣVn-1)
O lo que es lo mismo:
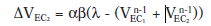
Como el EC2 no se ha presentado con anterioridad, no tiene fuerza asociativa aun, y su valor inicial V es 0.Pero la fuerza asociativa del EC1 es máxima (V=1) debido a la primera fase de condicionamiento, por lo que ΔV EC2 sería:
El incremento de la fuerza asociativa entre el EC2 y el EI durante este primer ensayo es inexistente. El modelo lo explica por la ausencia de sorpresa, ya que el EI ya era predicho por el EC1 por tanto su aparición no produce sorpresa alguna en los ensayos compuestos. No es necesario aprender nada sobre la relación EC2-EI para anticipar el EI: se está produciendo un bloqueo en la adquisición de dicha asociación.
Extinción
Este modelo también explica la extinción: recordemos que se puede extinguir la RC ocasionada tras el aprendizaje EC-EI si se presenta repetidamente el EC sin ir seguido del EI.
En el caso de la formula, esto es lo mismo que hablar de un EI que tienen intensidad cero (λ=0), por eso el primer ensayo de extinción tras la adquisición se plasmaría asi:
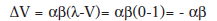
El incremento de la fuerza asociativa (ΔV) es en realidad un decremento, ya que es un término negativo. A medida que transcurren los ensayos, el valor de V va reduciéndose, hasta que no hay más sorpresa (el término (λ-V) se acerca a 0) y la asíntota se acerca a cero:
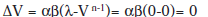
El modelo se apoya formalmente en la idea de que la excitación y la inhibición son extremos contrarios de un continuo, por tanto la extinción consiste en un desaprendizaje según este modelo. Éste enfoque no es correcto porque no se ajusta a lo que se conoce como la extinción
Inhibición condicionada
En este fenómeno un EC predice la ausencia de la aparición posterior de un EI. En este caso durante la fase de entrenamiento un EC1 es emparejado con un EI hasta llegar a la asíntota del aprendizaje (V=1). En la segunda fase, ese mismo EC1 se empareja con el EC que va a convertirse en inhibitorio (EC2) siendo ambos seguidos de la ausencia del EI. Ocurre lo siguiente:
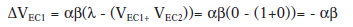
Esto indica que la fuerza asociativa del EC1 irá decreciendo a medida que aumentan los ensayos en compuesto, hasta llegar a 0.
Según este modelo, en el caso de entrenamientos en compuesto los EC excitatorios suman fuerza asociativa, mientras que los inhibitorios la restan.
Problemas del modelo
Aunque se trata de un modelo de referencia, tiene una serie de limitaciones que deben tenerse en cuenta:
1. La extinción de la inhibición condicionada
Este modelo afirma que si se presenta repetidamente un inhibidor condicionado sin ir acompañado del EI (es decir λ=0) la inhibición se extinguirá. Si aplicamos la formula a esta fase de extinción de la inhibición, el incremento de la fuerza asociativa del EC inhibitorio sería positivo en el primer ensayo:
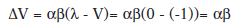
Lo que según este modelo, hará que el EC anteriormente inhibidor se convierta en excitatorio poco a poco. Pero esto no ocurre en realidad. Ciertas investigaciones muestran que no presentar el EI tras un EC inhibitorio, puede aumentar sus propiedades inhibitorias. Es posible que el error del modelo este en considerar la excitación y la inhibición como procesos opuestos y de signo contrario.
2. La inhibición latente (preexposición al EC)
Este modelo no puede explicar el efecto de inhibición latente en el que un EC es preexpuesto sin ir seguido de un EI para aparecer juntos en una fase posterior. Para este modelo, como el EI no aparece ni es esperado durante la fase de preexposición al EC, no hay asociación EC-EI y el valor de V no varía, siempre es 0, por lo que no debería afectar al aprendizaje en la fase de condicionamiento
Durante la fase de preexposición al EC:
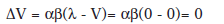
Entonces, en el primer ensayo de condicionamiento tras la preexposición, según este modelo.
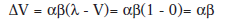
Sin embargo los datos muestran que, el aprendizaje de dicho condicionamiento se ve retrasado por la previa preexposición al EC, no comportándose como el modelo predice.
3. Bloqueo
Aunque el diseño experimental usado en el efecto de bloqueo suele tener como resultado menor RC como respuesta al EC bloqueado, a veces se da el efecto contrario, llamado aumentación o contrabloqueo. Consiste en un aumento de la RC ante el EC2 presentado en conjunto con el EC1.
El modelo Rescorla-Wagner no puede dar una explicación satisfactoria a este fenómeno, ya que predice que la aparición del EC2 no produce ninguna sorpresa en los ensayos compuestos ya que el EI era predicho con efectividad por el EC1, y por lo tanto no se aprende nada de la relación EC2-EI.
4. Extinción de la excitación condicionada
Este modelo explica la extinción como un desaprendizaje, pero no es una explicación correcta.
Fenómenos como la recuperación espontánea, renovación o la reinstauración muestran que la extinción no es un desaprendizaje ni lo contrario a la adquisición, sino un aprendizaje distinto.
Tampoco explica otros fenómenos relevantes como el precondicionamiento sensorial, la habituación, o la irrelevancia aprendida
La importancia del contexto
En la importancia del contexto en la manifestación del RC, resalta el hecho de que el EC y el EI no se presentan de forma aislada a otros estímulos durante el condicionamiento, sino que lo hacen dentro de un contexto específico (ej. Caja de Skinner) Los estímulos propios del contexto en el que se realiza el entrenamiento, son claves que el animal aprende junto con el EC. Se podría considerar que estas claves contextuales son entrenadas en compuesto con el EC, sirviendo de ECs de mayor duración y produciendo efectos similares al bloqueo o ensombrecimiento. Lo mismo ocurre cuando el EI se presenta en ausencia del EC: lo hace dentro de un contexto con diferentes claves, quedando asociado al mismo.
Teniendo en cuenta esto, lo tipos de contingencias del apartado 2.1 se pueden describir en relación a los estímulos del contexto que condicionan la relación EC-EI.
Conforme a la presencia o ausencia del EC en un ensayo de condicionamiento, podrían ocurrir dos tipos de ensayos distintos:
- Ensayos de condicionamiento EC-EI cuando el EC (junto con el contexto) va seguido del EI
- Momentos entre ensayos de condicionamiento, en los que en espera del inicio del siguiente ensayo solo están presentes las claves del contexto y el EI.
Cuando la proporción de veces en las que el EC, junto al contexto, van acompañados del EI es mayor que las que sólo lo está el contexto, se dará una contingencia positiva EC-EI. Por el contrario si la probabilidad de aparición del EI en presencia de sólo el contexto (sin el EC) es mayor, la contingencia EC-EI será negativa. Si la proporción de veces entre ambas situaciones es similar, la contingencia percibida será nula.
Hipótesis del comparador
Esta hipótesis propone que la RC no solo depende de la asociación EC-EI, sino también del resto de asociaciones presentes en ese momento que puedan establecerse entre las claves del contexto y el EI.
El sujeto en un ensayo de condicionamiento aprende dos cosas: que el EC y el EI están asociados, y que las claves contextuales y el EI también lo están. La comparación entre ambos tipos de asociaciones será determinante para el nivel de respuesta al EC.
Si la fuerza asociativa de EC-EI es mayor que aquella que presentan la asociación entre claves de contexto y EI; la RC tendrá lugar (contingencia positiva).
En cambio si la asociación EC-EI es más débil que la asociación entre claves del contexto y EI; no se mostrará la RC esperada ante el EC. Ocurre porque el animal percibe como mayor la probabilidad del EI en presencia del contexto y no del EC (contingencia negativa).
Es decir, si el valor excitatorio de las claves del contexto es mayor que la del propio EC, se dará una RC inhibitoria ante dicho EC. De la misma forma, si las dos asociaciones son comparables en fuerza, la contingencia será nula, y de nuevo la RC frente al EC no tendrá lugar.
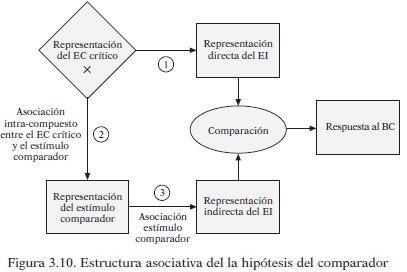
Esta hipótesis asume que el animal puede aprender tres tipos de asociaciones durante el condicionamiento (mirar el esquema de arriba): EC-EI (1); EC y claves de contexto (2); claves de contexto y EI (3).
Cuando se presenta el EC este activa dos tipos de representaciones del EI: directas, tras aparecer el EC (1) e indirectas por las asociaciones creadas con el contexto tanto con el EC como con el EI (2) y (3). La comparación entre las asociaciones directas e indirectas será lo que determine la intensidad de la RC y su carácter excitatorio o inhibitorio. Esta teoría tiene dos premisas a destacar:
- No existen las asociaciones inhibitorias, ambas son asociaciones excitatorias del EI, ya sea con el EC o con el contexto. Por eso la manifestación final de la RC depende de la fuerza relativa de la asociación EC-EI (1) con respecto a las asociaciones excitatorias entre el contexto y el EI (2) y (3)
- La comparación entre las asociaciones excitatorias que se forman durante el condicionamiento, determina la manifestación de la RC, pero no el aprendizaje. Se hace la comparación una vez terminado el entrenamiento. Por eso mismo si se da un cambio en la fuerza asociativa del contexto después del aprendizaje, esto cambiará la forma en la que se responde al EC. Explica las diferencias en la RC como diferencias en la ejecución, efectos como el bloqueo serían fallos de ejecución, no de aprendizaje.
Modelos atencionales
Teoría de Mackintosh
Esta teoría no se basa en la ausencia de sorpresividad del EI para explicar el CC y los fenómenos como el bloqueo, sino en el papel de la atención en el aprendizaje.
Mackintosh y Turner hicieron el siguiente experimento: presentaron a dos grupos, experimental y control, un sonido seguido de una descarga eléctrica en la primera fase. En la fase 2 se llevó a cabo el bloqueo, en el grupo experimental, presentando dicho sonido con una luz novedosa, seguido el compuesto de la descarga. En la fase 3 a ambos grupos se le presenta el compuesto luz+sonido seguidos de una descarga de mayor duración. Los resultados mostraron que en la fase 3, el grupo de control aprende que cuando la luz está presente la intensidad de la descarga aumenta. En cambio, el grupo experimental aprende en la fase 2 que la luz es redundante, que no es necesaria para predecir la descarga, y dejan de prestarle atención, lo que hace que no aprendan nada de dicho EC durante la fase 3.
Este modelo muestra que dicho efecto se debe al hecho de que los animales ignoran los estímulos predictores redundantes, en contra de la teoría Rescorla-Wagner que lo explicaba con la falta de sorpresividad.
La teoría Mackintosh tiene como base la idea de que la atención que se presta a un EC depende de lo efectivo que sea dicho EC prediciendo el EI. Cuanto mejor predictor sea, mayor atención le prestaremos.También depende dicha atención del resto de los ECs, como ocurre en el caso del bloqueo. Si nuestro EC no es mejor predictor del EI que los demás ECs, le prestaremos menos o ninguna atención.
Por tanto la atención aumentaría en los ensayos en los que el EC es un buen predictor del EI, y disminuye en aquellos en los que no lo es tanto. Esta teoría atencional puede explicar algunos efectos para los que el modelo Rescorla-Wagner no es capaz de ajustarse al comportamiento real mostrado por los sujetos, como el caso de la inhibición latente. Mackintosh explica este efecto basándose en la falta de atención al EC irrelevante durante la preexposición: como hemos dejado de prestarle atención al EC en la fase que no predice el EI, nuestro aprendizaje de asociación EC-EI será más lento.
Teoría de Pearce-Hall
Esta teoría atencional afirma que, en un contexto de aprendizaje, no debemos malgastar recursos prestando atención a estímulos que conocemos bien, pero sin embargo, si debemos prestar atención a aquellos que todavía no controlamos con seguridad, es un poco la explicación contraria a la de Mackintosh.
Según esta teoría, prestaremos cada vez menos atención a un EC en la medida en que con cada ensayo de condicionamiento se convierta en mejor predictor del EI. Si el EI tras el EC no resulta sorprendente, prestamos menos atención a dicho EC en el siguiente ensayo. Si nos resulta sorprendente, nuestra atención aumentará. Ambos autores aportan datos empíricos que apoyaron sus teorías.
Otras teorías
Hay numerosas teorías que tratan de explicar el CC desde distintos puntos de vista.
Una de las más completas es el modelo SOP (Wagner) y sus versiones posteriores. Este modelo extiende la teoría de Rescorla-Wagner teniendo en cuenta marcos de referencia, como la relación entre la memoria a corto y largo plazo (MCP y MLP) y el aprendizaje. Wagner sugiere que un estímulo sorprendente tiene mejor procesamiento en nuestra MCP y por lo tanto mayor probabilidad de mantenerse en nuestra MLP.
Dentro de nuestro sistema de procesamiento de la información, un estímulo nos resulta sorprendente si no está presente en nuestra MCP. Por tanto el aprendizaje depende de que el EI sea sorprendente, pero la sorpresa se ve reducida si el estímulo ya está activado en nuestra MCP cuando se presenta físicamente.
El modelo SOP representa el condicionamiento utilizando nodos y redes neuronales, herramientas propias del conexionismo. Wagner asume que el condicionamiento da lugar a una asociación entre la representación (denominada nodo) del EC y la del EI. Las asociaciones entre nodos se conocen como conexiones. Los nodos del EC y el EI se activan cuando los estímulos reales lo hacen, y ocurre a dos niveles distintos de intensidad:
- A1: estado en el que el nivel de activación es alto y la atención que se presta al estímulo también lo es. Es un estado inicial, el nodo sólo puede mantenerse en A1 un breve intervalo de tiempo. Es necesaria la presencia real del estímulo para su activación.
- A2: el primer estado decae a este, con un menor nivel de activación, relacionado con una atención más periférica y menos focalizada. El nodo puede mantenerse en este estado un largo periodo de tiempo hasta volver a un estado de inactivación
El modelo describe que la asociación entre dos nodos, los correspondientes al EC y EI, solo tendrá lugar si ambos están activados, es decir, en el estado A1, ya que ambos deben coincidir en la MCP. La coincidencia de ambos nodos en A1 ensayo tras ensayo hace que la asociación entre ambos sea cada vez más fuerte.
Una vez que están asociados, la activación del que representa al EC tendrá como consecuencia la activación del nodo del EI, pero no en su máximo nivel, si no en el estado A2. El nodo EI solo se activaría en estado A1 ante la presencia real de dicho EI.