Una decisión es una respuesta a una situación en la que existe más de un curso posible de acción: opción o alternativa de elección. Suele basarse en las expectativas que tenemos sobre la ocurrencia de futuros acontecimientos y en la evaluación de las consecuencias de dichos acontecimientos en función de nuestras metas y valores. Por ejemplo, llegamos de una jornada de trabajo agotados y nos invita un amigo a ir al cine. Ante tal situación se ha de elegir el quedarse en casa descansando o ir a ver la peli en buena compañía, pero con el riesgo de dormirnos en la misma. Los cursos de acción serían: Ir al cine o quedarnos en casa. A la vez tenemos unas expectativas de lo que puede ocurrir:
- si nos quedamos, descansar y no ver una peli.
- elegir ir al cine, y puede ocurrir que veamos la película o que no por quedarnos dormidos en la misma.
Desconocemos la probabilidad de ocurrencia de estos acontecimientos pero podemos estimar su probabilidad y así evaluaremos sus consecuencias. En una escala de satisfacción entre 0 y 100:
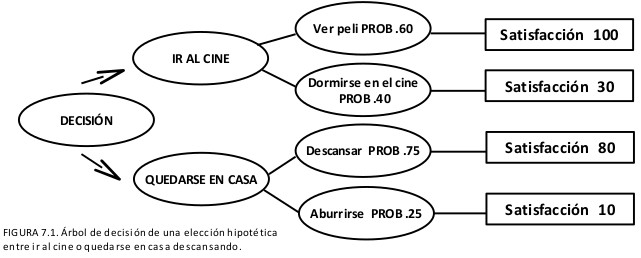
En el diagrama en forma de árbol de decisión de la situación estamos combinando las propias expectativas con los intereses y los deseos personales. El árbol de decisión no porporciona una solución pero sí la representación de las expectativas sobre la ocurrencia de los hechos futuros y de la evaluación de sus consecuencias. Ello permite visualizar gráficamente cuál es la alternativa que brinda una mayor satisfacción y su expectativa según nuestros criterios.
En la toma de decisiones se suelen diferenciar tres situaciones relacionadas con las expectativas:
- aquellas en las que se conocen las probabilidades (comprar un billete de lotería)
- en las que se desconocen y éstas se pueden estimar (seguir trabajando o poner negocio propio) y
- situaciones en las que hay certeza sobre las opciones y sólo se ha de elegir entre las mismas (pedir carne o pescado en el restaurante)
La certeza indica que no hay dudas sobre los acontecimientos futuros y la decisión se toma bajo este supuesto.
Las expectativas: el grado de creencia o probabilidad de que ocurra un acontecimiento concreto. Generadas éstas, se evalúan sus consecuencias asociadas en función de criterios personales. Se considera que la decisión se toma en un contexto de riesgo cuando se conocen las probabilidades, en un contexto de incertidumbre cuando éstas se estiman y en uno de certidumbre cuando se conoce con seguridad la ocurrencia.
La teoría normativa asume que cuando decidimos, lo hacemos eligiendo aquello que tiene el máximo valor en los resultados que se esperan obtener. Unos matemáticos del XVII y XVIII consideraron estudiar la probabilidad y la toma de decisiones en los juegos de azar como pauta de comportamiento óptima. El objetivo era encontrar la forma de cuantificar el valor de una apuesta en los juegos o en decisiones bajo condiciones de riesgo. Bajo este supuesto se denominaron Modelos del valor esperado coincidiendo este valor con la esperanza matemática el juego.
El Valor esperado de una alternativa es la suma del producto de c/valor por su probabilidad de ocurrencia. La mejor elección será aquella que obtenga el máximo valor esperado:
Alternativa 1 > Ganar 1000 euros con prob. 0.90 y ganar 0 euros con probabilidad de 0.10
[(1000 x 0,90) + ( 0 x 0,10) = 900 euros]
Alternativa 2 > Ganar 500 euros con prob. 0.80 y ganar 20 euros con probabilidad de 0,20
[(500 x 0,80) + ( 20 x 0,20) = 404 euros]
La alternativa 1 es la mejor porque tiene un valor esperado de 900 euros frente a 404 de la 2a.
Esta cantidad es promedio ponderado de los resultados que se esperan ocurran en el futuro. Se pondera cada resultado posible con respecto a la frecuencia con que se espera. También se puede obtener a partir de estimaciones subjetivas, y es el valor esperado la representación de las creencias personales sobre la ocurrencia del posible resultado.
Según la teoría del valor esperado los sujetos buscan maximizar sus ganancias y elegirán la opción 1. No obstante, no todos se ajustan a la elección y prefieren la opción 2, en la que se gana menos pero se gana siempre. Ello hizo que el “valor esperado” fuera sustituido por el concepto de la utilidad esperada, entendida como el grado en que las consecuencias de una opción alcanzan las metas personales en una situación determinada.
La primera objeción a este criterio fue en el siglo XVIII (Nicolás Bernouill) aunque fue Daniel Bernouilli el que desarrolló y lo publicó como Paradoja de San Petersburgo. Trata de la decisión de un jugador ante un juego con valor esperado infinito:
- El jugador A plantea las reglas del juego y el jugador B tiene que decidir cuánto dinero está dispuesto a pagar por participar en él.
- La regla consiste en que el jugador A lanzará una moneda hasta que caiga el lado de la cara, y el número de veces necesarios (n) para conseguirlo determinará la cuantía del premio.
- Si A lanza una moneda y sale cara en la primera tirada, el jugador B pagará dos ducados y termina el juego.
- La pregunta que se plantea en la paradoja es: ¿cuánto pagaría el señor B al jugador A por participar en este juego?
Según el criterio del valor esperado, el jugador B debería participar en el juego si el valor esperado es mayor que la suma exigida para entrar a jugar y rechazar la propuesta cuando ésta sea menor.
Para calcular el valor esperado total del juego se suman todos los valores esperados en cada lanzamiento, dando como resultado un número infinito de “ducados”. La paradoja surge porque con un valor infinito se debería apostar cualquier cantidad de dinero. Al señor B le interesa que salga cara lo más tarde posible. Los resultados evidenciaron que grlmente no están dispuestas a apostar más de 20 monedas por participar. Pone de manifiesto que no es realista asumir que B espere poder jugar durante tiempo ilimitado para obtener número infinito de monedas a cualquier precio.
Para resolverlo, Daniel Bernoulli propuso la noción de utilidad esperada como valoración subjetiva de las posibles consecuencias monetarias del juego. Es en función de la riqueza de cada individuo y está en relación inversa a su nivel de riqueza. Ganar o perder 200 euros no es lo mismo para un rico que para un pobre, y cuánto más dinero se tenga menos se valorará dicha ganancia o pérdida. El autor también comenta de utilidad marginal decreciente al señalar que la función de utilidad es siempre creciente pero crece cada vez más despacio. Es necesario diferenciar entre el valor esperado (cantidad objetiva) y la utilidad esperada que depende de las circunstancias de cada una.
En la paradoja descrita los individuos están dispuestos a pagar distintas cantidades por participar en el juego según su criterio, aunque el valor esperado sea infinito. Esta distinción permite analizar la toma de decisiones bajo riesgo considerando las valoraciones subjetivas que hacemos.
Bernouilli logró demostrar que el valor del dinero no es lo mismo para todos y que dicha valoración es en proporción a la utilidad que pueden obtener de él.
2.1. Teoría de la utilidad esperada
El concepto de utilidad esperada de Bernoulli fue retomado por Neumann y el economista Oskar Morgenstern (1944). La teoría de la utilidad esperada de Neumann y Morgenstern ha sido el modelo estándar de la decisión individual en situaciones de riesgo. Esta teoría del ámbito de la economía está interesada en “qué” deciden las personas más que en “cómo” deciden. Su interés se centra en el análisis de la relación entre aquello que se decide y los valores personales que le han llevado a ella. El resultado del análisis permite entender los actos de elección como las actitudes que tiene una persona hacia el riesgo.
Los autores proponen unos axiomas que garantizan la coherencia en el proceso de toma de decisiones. Se necesita una escala de preferencias con la que poder evaluar las opciones. La noción de utilidad es la escala de preferencias con mayor aceptación de los modelos normativos.
Con esta se está asumiendo que las metas u objetivos de las personas se expresan en su preferencias, buscando resultados acordes con los valores que se tienen.
Se asume que los atributos de una opción son independientes y que cada uno tiene un peso o importancia. Implica ello que cada uno tiene una utilidad que indica el grado en que esa propiedad contribuye a alcanzar las metas y objetivos. Las personas conocen su entorno, son capaces de ordenar las alternativas según el criterio de utilidad y eligen la de mayor proceso de maximización. La decisión óptima será aquella que refleje sus preferencias. Esta teoría presenta las siguientes ventajas:
- consideración de toda la información disponible sobre las diferentes opciones,
- comparación entre cualquier par de opciones dado que comparten una misma escala de preferencias y
- establecimiento de una estructura de preferencias coherente a partir de la determinación de utilidad de cada opción.
2.1.1. Los axiomas de la teoría de la utilidad esperada
Esta aproximación ofrece un conjunto de axiomas para poder construir una escala de utilidades en la que la representación de los valores de las consecuencias se ajuste a una concepción ordinal de la utilidad. Los axiomas son principios fundamentales e indemostrables sobre los que se construye una teoría. Son proposiciones claras y evidentes que se admiten sin demostración, pero pueden no serlo. Lo que sí, su expresión lógica se utiliza para la deducción y así poder generar conceptos a partir de ellos.
Savage 1954 generalizó la teoría de la utilidad esperada para permitir la inclusión de las probabilidades subjetivas basadas en las creencias propias u opiniones sobre probabilidad de los hechos. Edwards 1954 denomina a esta ampliación “el modelo de la utilidad subjetiva esperada” en un artículo que fue el primer intento de la psicología por acercarse a este dominio.
Sin embargo no es habitual hacer una distinción porque los axiomas y teoremas sistematizados de Savage cumple las leyes de la teoría de la utilidad esperada y las probabilidades subjetivas que contempla, cumplen las leyes de la probabilidad.
Axiomas:
- Axioma de completitud u ordenamiento completo: A > B; B > A ; A ≈ B
- A se prefiere a B A= pera B = piña
- B se prefiere a A
- se prefieren las dos, y por tanto, son indiferentes
- ante un conjunto de alternativas, las personas pueden ordenarlas según las preferencias asumiendo que es posible ser indiferente. Esto se hace explícito ante dos alternativas donde “no se puede decidir” dejar de decidir. Estas serían comparables y la persona ha de preferir una de ellas o considerarlas como equivalentes.
- Axioma de transitividad: Si A > B y B > C, entonces A > C
- Permite relacionar el orden de preferencias entre 2 alternativas a través de una tercera en común. Este orden debe ser coherente o consistente entre sí. Si se prefiere A respecto a B, y la alternativa B respecto a C, se deberá preferir A respecto a C. Se prefiere piña como postre. El camarero indica que de no haber podría elegir entre pera o manzana. Si se responde pera, se establece un orden, donde se prefiere la piña a la pera y esta a la manzana o bien que se prefiere siempre piña respecto a la manzana.
- Axioma de cierre: si A y B son alternativas de un conjunto S, entonces ApB también lo son
- Enuncia la capacidad de las personas para conceptualizar las probabilidades asociadas con las alternativas. Si A y B son alternativas de un conjunto S, entonces la probabilidad dela alternativa A (p) y la probabilidad de la alternativa B (p-1) también forman parte de ese conjunto. En ApB se considera implícita la probabilidad de la alternativa B(1-p) dado su complementariedad.
- Axioma de reductibilidad: [(ApB)qA'] ≈ (ApqB)].
- Este introduce la distribución de probabilidades entre alternativas para poder descomponer una alternativa compuesta en una simple. Alguna de sus consecuencias es también una alternativa. Las reglas de la probabilidad permiten reducir toda alternativa compuesta a una simple que sea equivalente.
- Axioma de independencia: A > B si y solo si (ApC) > (BpC)
- El orden de preferencias entre dos alt simples no cambia por la adición de una nueva alternativa. Por ejemplo, si preferimos piña a pera ( A > B) como postre, entonces deberíamos preferir una alternativa compuesta por piña y naranja (ApC) frente a otra compuesta de pera y naranja. (BpC)
- Axioma de consistencia: A > B si y solo si A > (ApB) > B
- Axioma básico y nos indica que si la alternativa A se prefiere a B, entonces la A se prefiere siempre que se presente con cierta probabilidad.
- Axioma de continuidad: Si A > B > C, entonces existe una probabilidad p tal que B ≈ (ApC)
- Este es importante para la construcción de la escala de utilidad porque asume que habrá un valor entre 0 y 1 que permite que la persona sea indiferente. Se establece que si A es preferido a B y B es preferido a C, entonces siempre es posible encontrar una probabilidad p para que la alternativa B sea equivalente a la combinación de la probabilidad p de A con la probabilidad 1 – p de la alternativa C (ApC) Con esta se asegura que no haya una alternativa mejor o peor a las otras y se puede localizar en la escala la opción B entre A y C.
Cuando se cumplen estos axiomas la función de utilidad establece:
- x se prefiere a y si y solo si la utilidad de x es mayor o igual a y
- la utilidad de una alternativa es igual a la utilidad de cada resultad ponderada por su probabilidad.
A partir de estas dos propiedades se puede construir la curva de la función de utilidad.
Supongamos:
- Opción A: una ganancia segura de 240 euros.
- Opción B: un 25% de probabilidades de ganar 1000 euros y un 75 % de ganar 0 euros.
Si eligen la A, sabemos que han asignado una utilidad mayor al valor esperado de 240 euros que al valor esperado de 250 euros: 25% s/1000 + 75% s/0 = 250 euros.
Si la utilidad esperada fuera proporcional a la cantidad del valor esperado, sería lineal y representaría una actitud neutral hacia el riesgo. La utilidad B U(B) sería = U(A) También encontramos personas que presentan preferencia por el riesgo al elegir situaciones con mayor riesgo por una mayor cantidad de dinero de de menor riesgo y menor cantidad de dinero.
Supongamos:
- Opción A : una ganancia segura de 260 euros.
- Opción B : un 25% de probabilidades de ganar 1000 euros y un 75 % de ganar 0 euros.
Su cálculo sería U(B) 25% s/ 1000 + 0,75% s/0 = 250 euros; utilidad de B la U(A) = U(260 euros) y eligen la utilidad de B.
La utilidad describe las preferencias de un sujeto y los axiomas imponen las restricciones sobre sus posibles relaciones, aunque no determinen cuáles son estas transferencias. Esta teoría proponía que para ser racionales en la toma de decisiones no había falta compartir la misma función de utilidad, sino que bastaba con ajustarse a los mismo axiomas normativos en esa búsqueda por alcanzar la máxima utilidad esperada que había sido definida individualmente.
2.2. Objeciones a la teoría de la utilidad esperada
Los axiomas anteriores fueron objeto de críticas entre las que destacan las paradojas de Allais 1953 y la de Ellsberg de 1961. Indicaban como se podían violar algunas de las restricciones impuestas, cuestionando así el concepto de racionalidad subyacente de la teoría.
La paradoja formulada por Allais se centra en la violación del axioma de independencia. Si una alternativa A se prefiere a B, entonces cualquier combinación de A y C con una probabilidad determinada debe ser preferida a otra combinación de B con C con la misma probabilidad. Allais describió dos situaciones:
Situación primera:
- Alternativa A: ganar 1 millón con p de 1 (con total certeza)
- Alternativa B:
- ganar 2,5 millones con probabilidad de 0,10
- ganar 1 millón con probabilidad de 0,89
- ganar 0 euros con probabilidad de 0,01
En esta primera la mayoría opta por la alternativa A en la que se gana 1 millón con certeza. Para hacer el cálculo de la utilidad esperada entre ambas alternativas se considera la ganancia de 1 millón eliminando la prob de la misma de la alternativa B y conservando la probabilidad restante en la alternativa B ( 1 – 0,89=0,11)
- Alternativa A: ganar 1 millón con probabilidad de 0,11
- Alternativa B: ganar 2,5 millones con probabilidad de 0,10 y ganar 0 euros con probabilidad de 0,01
Elegir la opción A implica que la utilidad U (A) 0,11 es mayor que la utilidad de la alternativa B , donde U(B) 0,25.
La paradoja se plantea cuando se presenta la segunda situación en la que las dos alternativas comparten una ganancia de 0 euros.
Situación segunda:
- Alternativa C: ganar 1 millón con probabilidad de 0,11; ganar 0 euros con probabilidad de 0,89
- Alternativa D: ganar 2,5 millones con probabilidad de 0,10; ganar 0 euros con probabilidad de 0,90
Considerando la ganancia común de 0 euros en C y conservando la probabilidad restante en la alternativa D (0,90 – 0,89 = 0,01) la situación sería:
- Alternativa C: ganar 1 millón con p de 0,11;
- Alternativa D: ganar 2,5 millones con probabilidad de 0,10; ganar 0 euros con probabilidad de 0,01
La mayoría de las personas prefieren la alternativa D inicialmente. Implica que U(C) 0,11 es menor que la utilidad de la alternativa D, U(D) 0,25
Savage 1954 hace un análisis de la paradoja de Allais ampliando el axioma de independencia con el principio denominado aspecto cierto (sure-thing). Este afirma que si dos alternativas comparten un resultado concreto, la preferencia será independiente del valor de este resultado común. Las personas descartan el resultado seguro y basarán su elección en los posibles resultados diferentes entre alternativas. Ante la situación primera, en una probabilidad de 0,01 se elegirá entre 1 millón y 0 euros; y ante la probabilidad de 0,10 entre 1 millón y 2,5 millones. Ante la situación segunda, el aspecto seguro es la ganancia de 0 con probabilidad de 0,89 y se rechaza, y sigue siendo la decisión entre 1 millón y 0 euros; y ante la probabilidad de 0,10 entre 1 millón y 2,5 millones.
La elección de las alternativas A y D contradice la coherencia del orden de preferencias. Es opuesta dependiendo de cómo se presente el problema, lo que contradice el principio descrito por la ta de la utilidad. En la primera situación, se prefiere la opción A con ganancia segura menor que en B en la que existe una probabilidad aún pequeña de quedarse sin nada. En la segunda situación, la pequeña diferencia existente entre probabilidades de las dos alternativas queda compensada por la gran diferencia entre ganancias. Se debe considerar la relación entre la probabilidad y la ganancia de un resultado y no sólo el valor absoluto de su producto como en la Teoría de la perspectiva.
La segunda paradoja planteada por Ellsberg 1961 se basa en el concepto de ambigüedad. Se extraen bolas de colores. 90 bolas: 30 rojas, 60 negras y amarillas en proporción desconocida. La extracción al azar supone ganancia distinta en función del color. Se presentan dos situaciones:
Situación 1
- Alternativa A: ganar 100 euros si la bola es roja; ganar 0 si es negra o amarilla
- Alternativa B: ganar 100 si es negra y 0 si es roja o amarilla
Situación 2
- Alternativa C: ganar 100 si la bola es roja o amarilla; ganar 0 si es negra.
- Alternativa D: ganar 100 si es negra o amarilla; ganar 0 si es roja.
La mayoría prefiere la opción A en la primera situación y la D en la segunda. La elección indica la preferencia por ganancias con probabilidades conocidas, evitando la ambigüedad de la probabilidad de obtener una bola negra o amarilla. También violan el axioma de independencia. El aspecto cierto entre las alternativas se encuentra en las bolas amarillas.
Por tanto la teoría de la utilidad esperada se ha descartado como modelo normativo válido de la toma de decisiones. Se puede considerar que es una guía prescriptiva adecuada o un buen criterio para el hombre racional, pero no un modelo descriptivo de decisiones. Analiza como debería de ser una decisión correcta, para una correcta planificación, inversión o estrategias políticas, pero no es buena descripción de las elecciones de las personas en su vida diaria.